Funkcja Kwadratowa Kalkulator
Naszkicuj wykres funkcji kwadratowej i oblicz jej miejsca zerowe, deltę oraz współrzędne wierzchołka.
ax2+bx+c
a=
b=
c=
Jeśli delta jest ujemna, miejsca zerowe funkcji nie istnieją- zatem kalkulator podaje wartość Nan.Wykres funkcji kwadratowej.
Wpisz różne wartości parametrów a,b,c i zobacz jak zmienia się wykres funkcji.
Jeśli korzystasz z telefonu, stuknij w wykres — aby zapobiec przesuwaniu ekranu.
Wykonaj gest palcami, aby przybliżyć lub oddalić wykres.
Warto zauważyć wpływ poszczególnych parametrów na wykres funkcji:
- Gdy a jest większe od zera, ramiona funkcji na wykresie są skierowane w górę.
- Gdy a jest mniejsze od zera, ramiona funkcji na wykresie są skierowane w dół.
- Parametr b przesówa wykres funkcji w lewo lub prawo.
- Parametr c przesówa wykres funkcji w górę lub w dół.
- Im bliższy zeru jest parametr a, tym szerszą parabolę uzyskujemy. Dla a równego zero uzyskamy funkcję liniową.
Funkcja kwadratowa miejsca zerowe
Miejsca zerowe funkcji kwadratowej, to wartości x, dla których funkcja daje wynik równy zeru. Inaczej mówiąc, jeśli weźmiemy wzór funkcji kwadratowej i w miejsce iksów podstawimy miejsca zerowe, to po wyliczeniu otrzymamy wartość równą zeru.
Miejsca zerowe funkcji kwadratowej na wykresie.
Patrząc na wykres funkcji kwadratowej, miejsca zerowe są to punkty, w których parabola przecina oś iksów. Zatem dana funkcja może mieć:
2 miejsca zerowe.
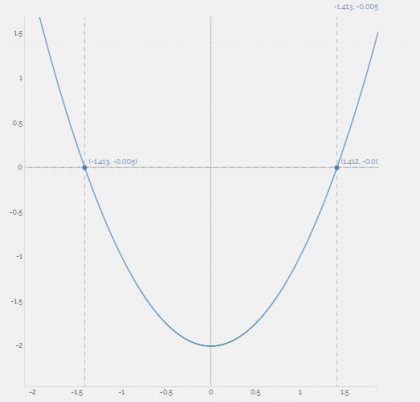
1 miejsce zerowe.
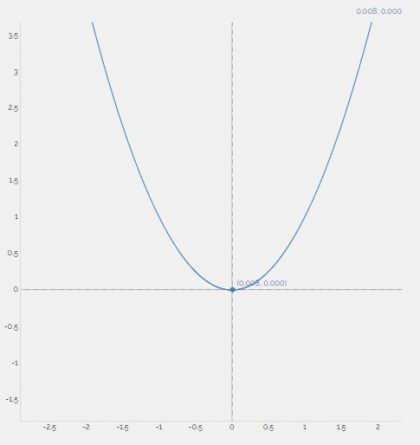
0 miejsc zerowych.
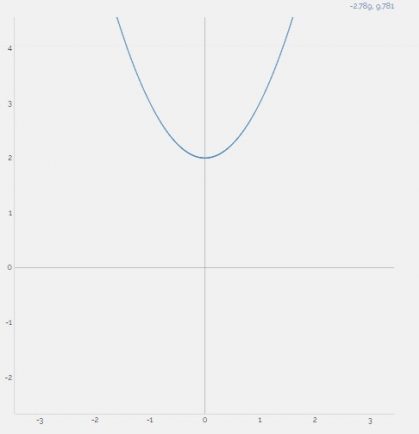
Jak policzyć miejsca zerowe funkcji kwadratowej ?
Krok 1.
Liczymy deltę.
Wzór na deltę :
.png)
Krok 2.
Liczymy miejsca zerowe.
Wzór na miejsca zerowe:
1).png) 2)
2)
.png)
jak widać, jeśli delta będzie równa zeru, 2 wzory dadzą ten sam wynik, gdyż pierwiastek z zera daje zero.
Jak policzyć wierzchołek funkcji kwadratowej bez wzoru ?
Wierzchołek ma współrzędne (p,q)
1. Liczymy punkt p.
P to wartość osi x.
Wiemy, że wierzchołek znajduje się po środku paraboli.
Zatem jest on w połowie drogi między pierwszym a drugim miejscem zerowym.
Aby znaleźć to miejsce, możemy użyć średniej arytmetycznej.
Zatem punkt p to średnia arytmetyczna dwuch miejsc zerowych.
średnią liczymy dodając te 2 wartości do siebie i dzieląc przez 2.
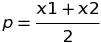
2. Liczymy punkt q.
Q to wartość osi y.
Zatem z definicji funkcji - znając wartość x możemy obliczyć odpowiadającą jej wartość y.
Podstawiamy wartość p pod wzór funkcji w miejsce x.
Po wyliczeniu otrzymamy wartość q.
Oczywiście można użyć gotowych wzorów na te punkty, jednak warto znać ten trik- gdyż daje on szersze pojęcie o istocie funkcji kwadratowej i pozwala ją lepiej zrozumieć.
Funkcja kwadratowa współrzędne wierzchołka wzory.
Wierzchołek ma współrzędne (p,q)
Wzór na współrzędną p:
.png)
Wzór na współrzędną q:
.png)
KATEGORIE

FINANSOWE
Znajdziesz tutaj wszystkie przydatne kalkulatory finansowe.

DO SZKOŁY
W tej kategorii znajdziesz kalkulatory, które przydadzą ci się w szkole, lub w innych projektach.

DLA DOMU
W tej kategorii znajdją się kalkulatory i narzędzia codziennego urzytku, które zaoszczędzą Ci czas i nerwy.
- Rachunek za Prąd.
- Opornik diody LED
- Kalkulator proporcji do skalowania przepisów.
- Więcej Już Niedługo !
O Nas
Jeśli szanujesz swój czas, i nie masz zamiaru pamiętać skomplikowanych wzorów- Ta strona jest do Ciebie! Znajdziesz tu wszystkie kalkulatory matematyczne jakie potrzebujesz - wszystko w 1 miejscu.
Nadal nie wiem jak policzyć ;_;
Jeśli nie znalazłeś kalkulatora którego potrzebujesz, lub masz pomysł na przydatne narzędzie- NAPISZ DO NAS. Chętnie wysłuchamy waszych propozycji i spróbujemy stworzyć odpowiednie narzędzie do tego celu.